Логарифмы — это математическая операция, обратная возведению в степень. Проще говоря, если у нас есть выражение a^b = c, то логарифм числа c по основанию a равен b. Это записывается как \log_a{c} = b.
Логарифмы играют важную роль в различных областях: от науки до финансов. Они помогают решить задачи, связанные с экспоненциальным ростом или убыванием, а также с упрощением сложных вычислений.
Применение логарифмов:
1. В математике и физике: Логарифмы используются для упрощения сложных выражений и уравнений, а также для решения задач, связанных с экспоненциальными функциями.
2. В статистике и экономике: Логарифмы помогают анализировать рост компаний, инфляцию и доходность инвестиций.
3. В науке: Они используются для анализа данных, связанных с биологическим ростом, химическими реакциями и радиационным распадом.
Пример задачи: Если популяция бактерий удваивается каждый час, через сколько часов она вырастет в 8 раз? Ответ: логарифм по основанию 2 от 8 равен 3, значит, популяция увеличится в 8 раз через 3 часа.
Логарифмы играют важную роль в различных областях: от науки до финансов. Они помогают решить задачи, связанные с экспоненциальным ростом или убыванием, а также с упрощением сложных вычислений.
Применение логарифмов:
1. В математике и физике: Логарифмы используются для упрощения сложных выражений и уравнений, а также для решения задач, связанных с экспоненциальными функциями.
2. В статистике и экономике: Логарифмы помогают анализировать рост компаний, инфляцию и доходность инвестиций.
3. В науке: Они используются для анализа данных, связанных с биологическим ростом, химическими реакциями и радиационным распадом.
Пример задачи: Если популяция бактерий удваивается каждый час, через сколько часов она вырастет в 8 раз? Ответ: логарифм по основанию 2 от 8 равен 3, значит, популяция увеличится в 8 раз через 3 часа.
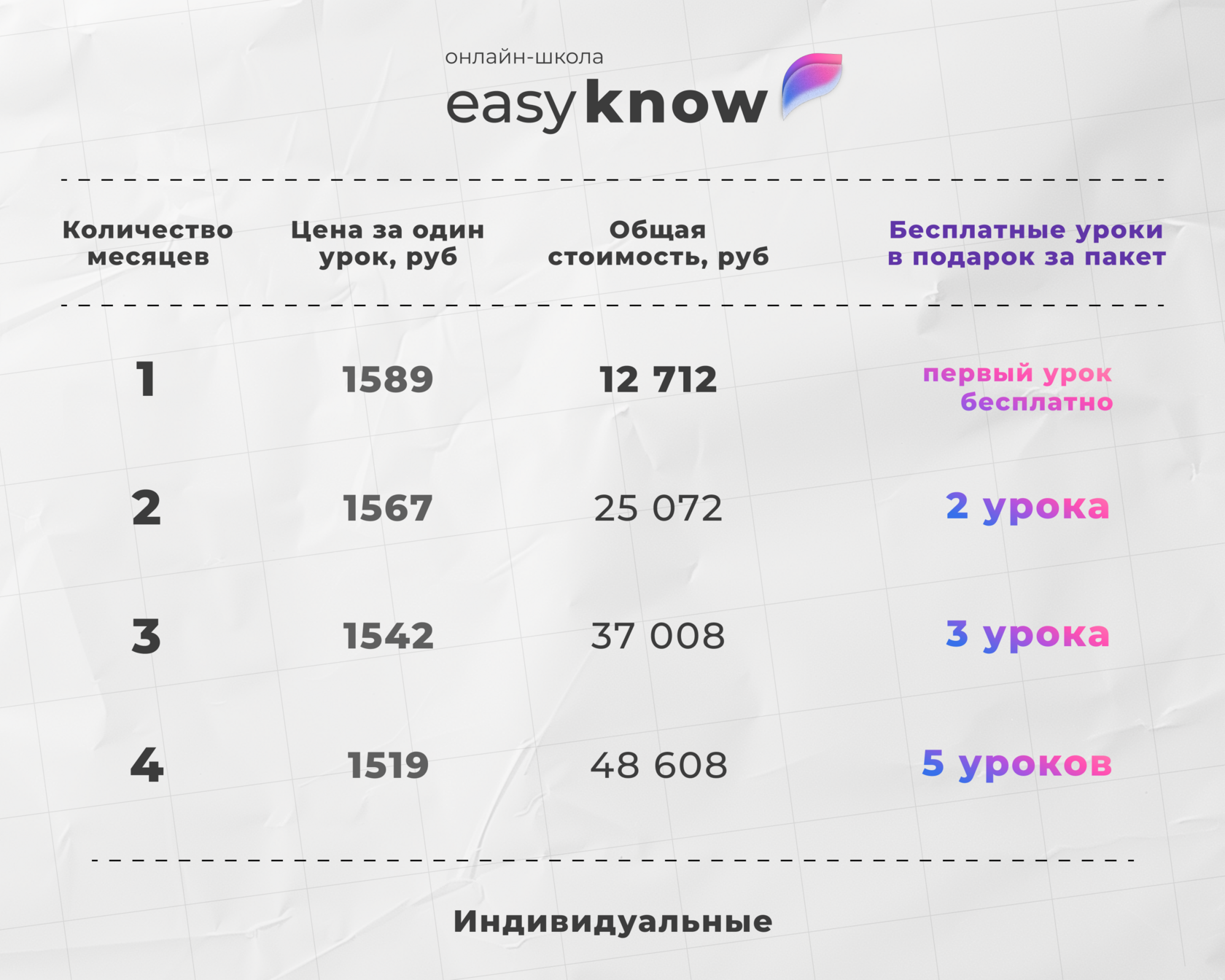
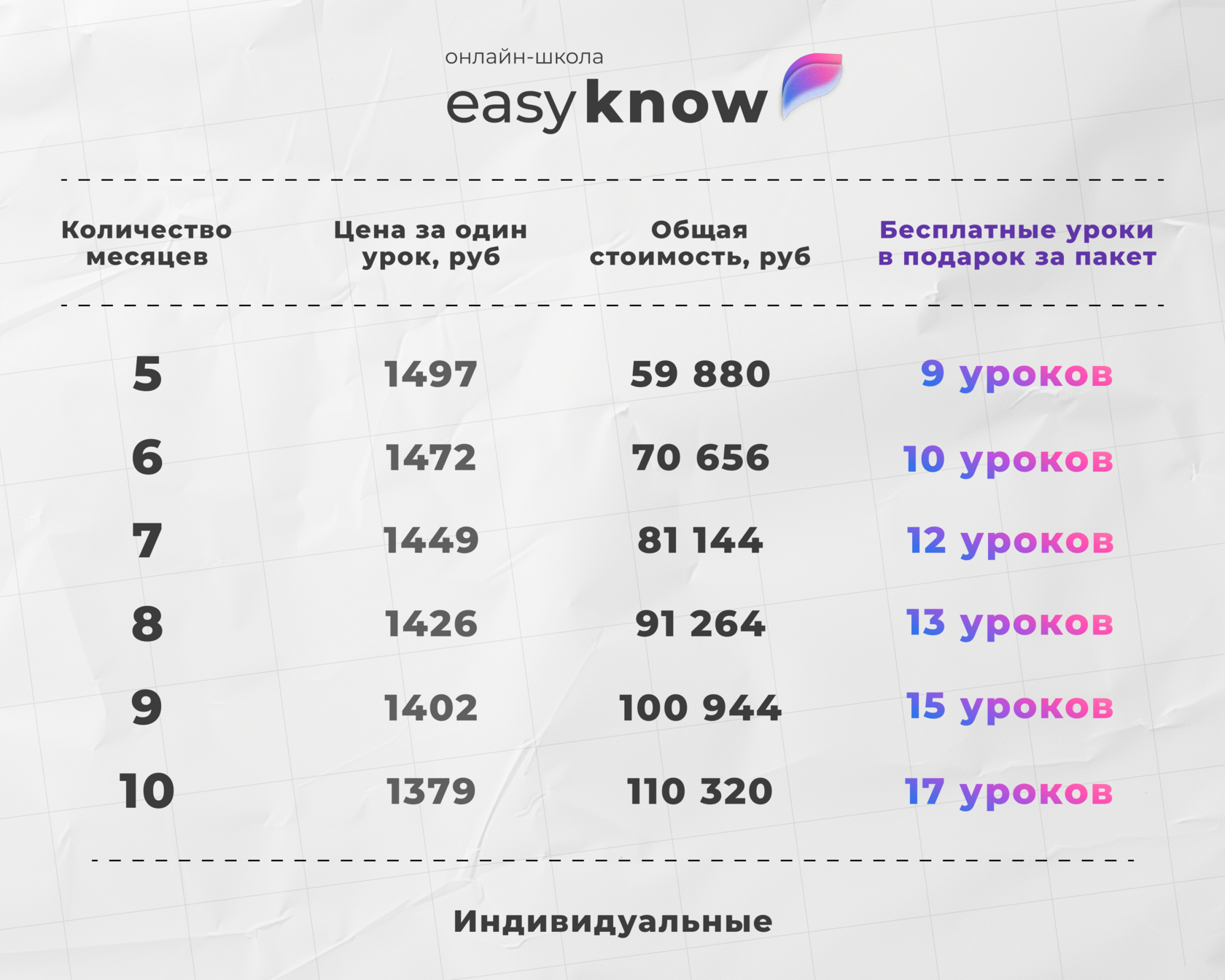
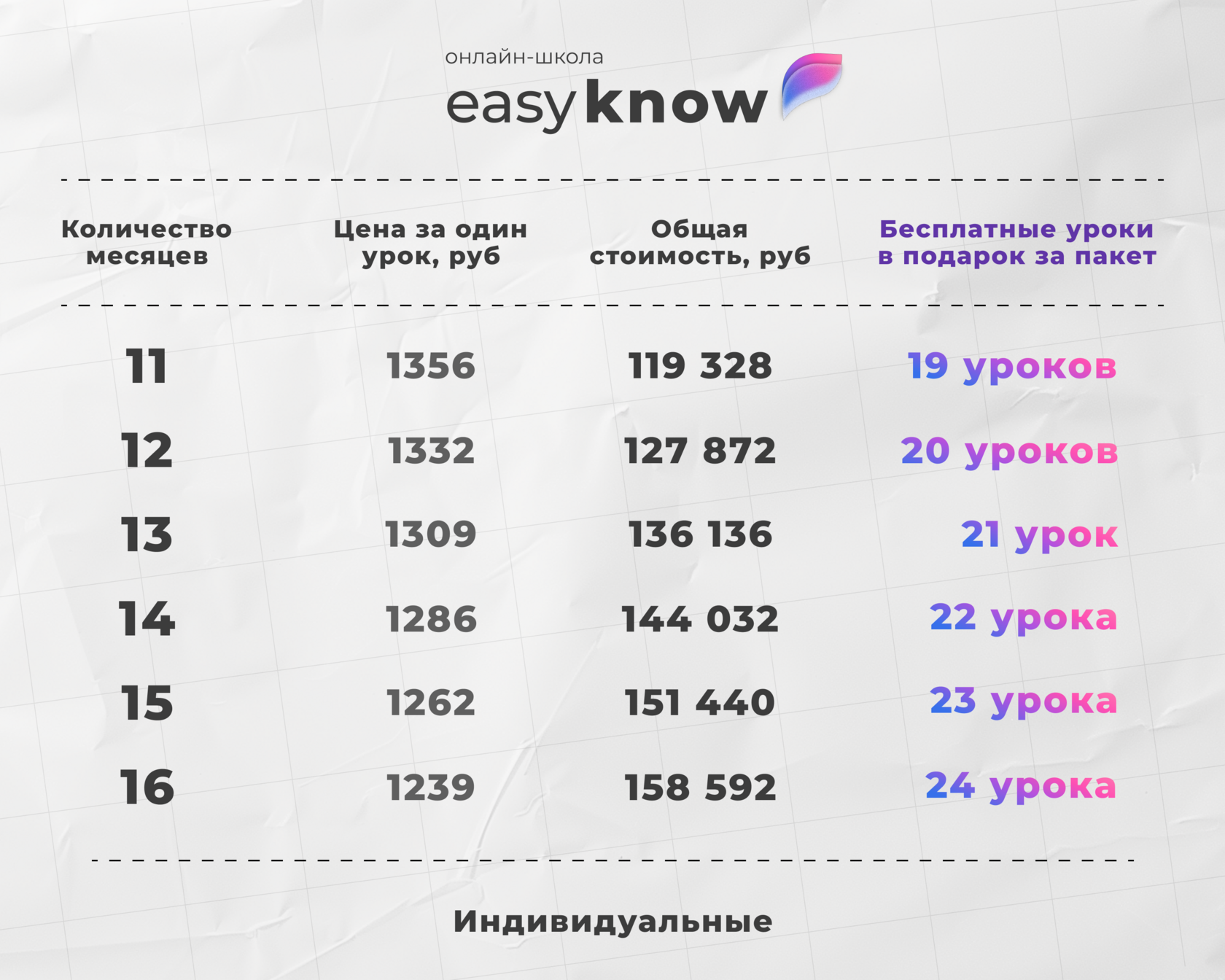
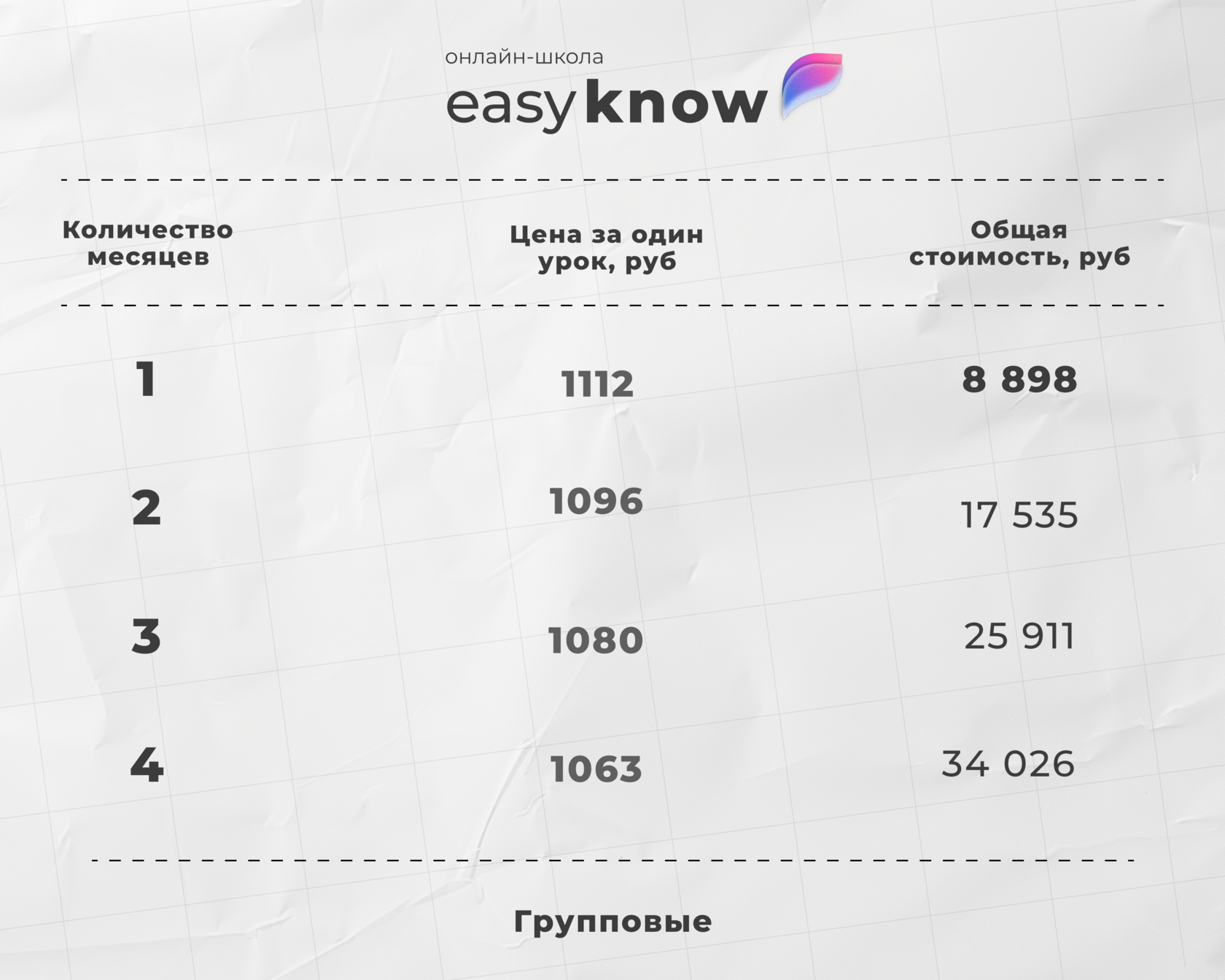
Подготовка с репетитором на образовательной платформе
- все материалы для подготовки к ЕГЭ по математике собраны в одном месте;
- репетитор помогает разобраться в сложных темах;
- образовательная платформа даёт доступ к тренировочным заданиям и разбору ошибок;
- можно выстроить план подготовки под конкретные цели и набрать высокие баллы.