Свойства логарифмов для ЕГЭ по математике

Логарифмы — важная тема как в профильной, так и в базовой математике. Они встречаются в заданиях части 1 и 2 на ЕГЭ, а знание их свойств помогает решать уравнения, неравенства и преобразовывать выражения.

Что такое логарифм

Логарифм числа b по основанию a — это показатель степени, в которую нужно возвести a, чтобы получить b:

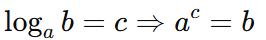
Пример:

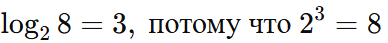
Основные свойства логарифмов для ЕГЭ

Как решать логарифмы по математике

Применяй свойства. Сначала упростить выражение, используя таблицу свойств.

Проверь область определения. Для логарифма:

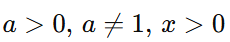
Преобразуй логарифмические уравнения к одинаковым основаниям.

Например:

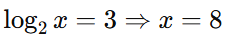
Для неравенств — помни, что если основание < 1, знак неравенства меняется.

Таблица логарифмов (основные значения)

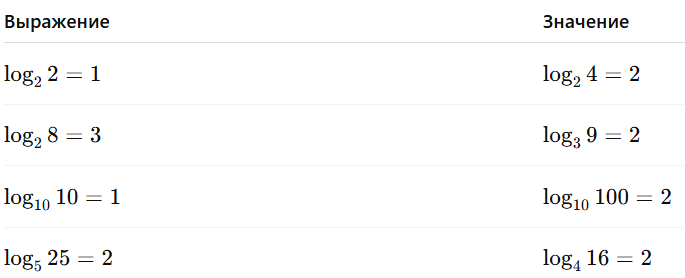
Подготовка к ЕГЭ по логарифмам

Повтори все свойства из таблицы.
Решай уравнения и неравенства на тренировочных вариантах.
Тренируйся на заданиях с параметрами (для профильного уровня).
Анализируй ошибки и смотри решения с комментариями.

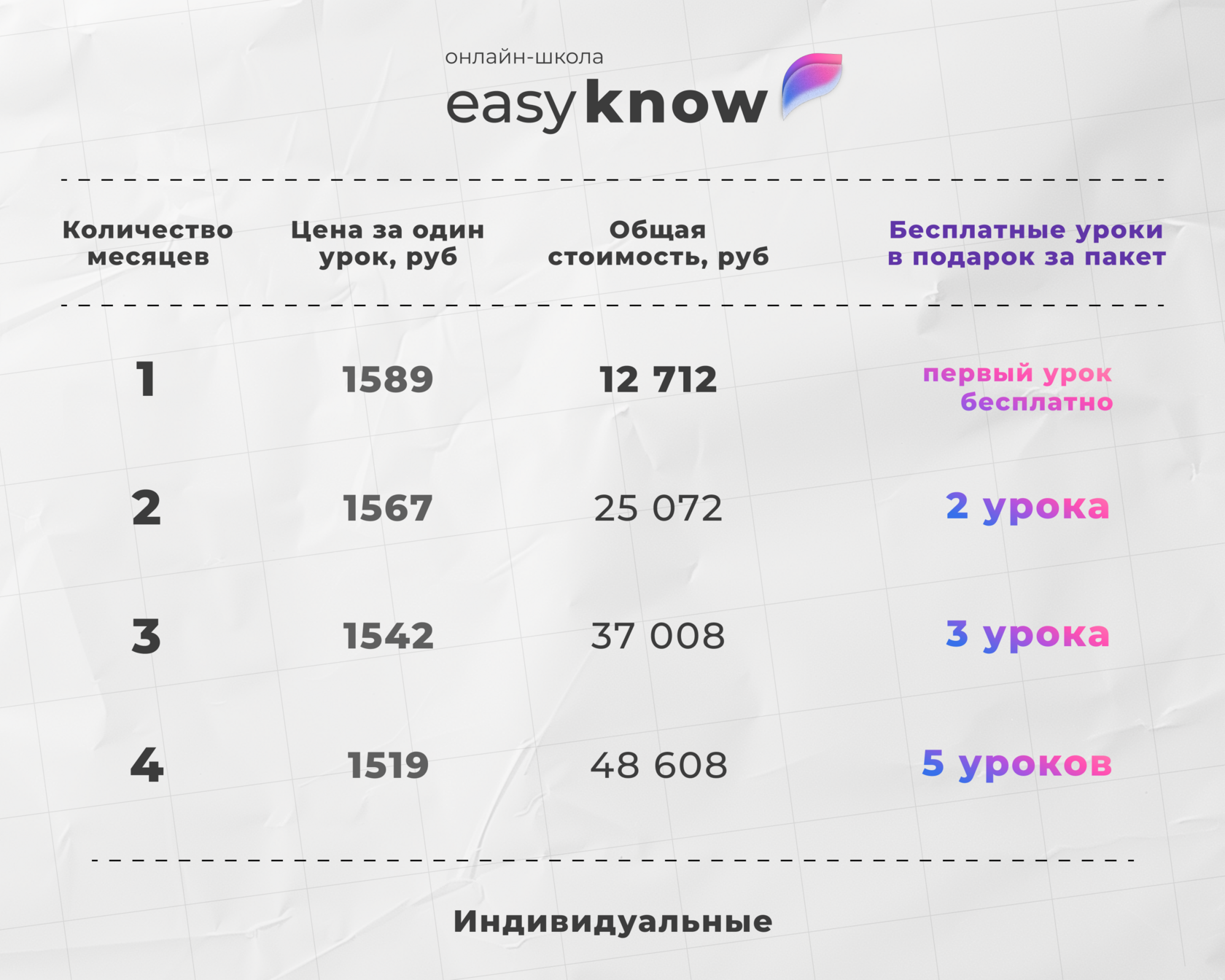
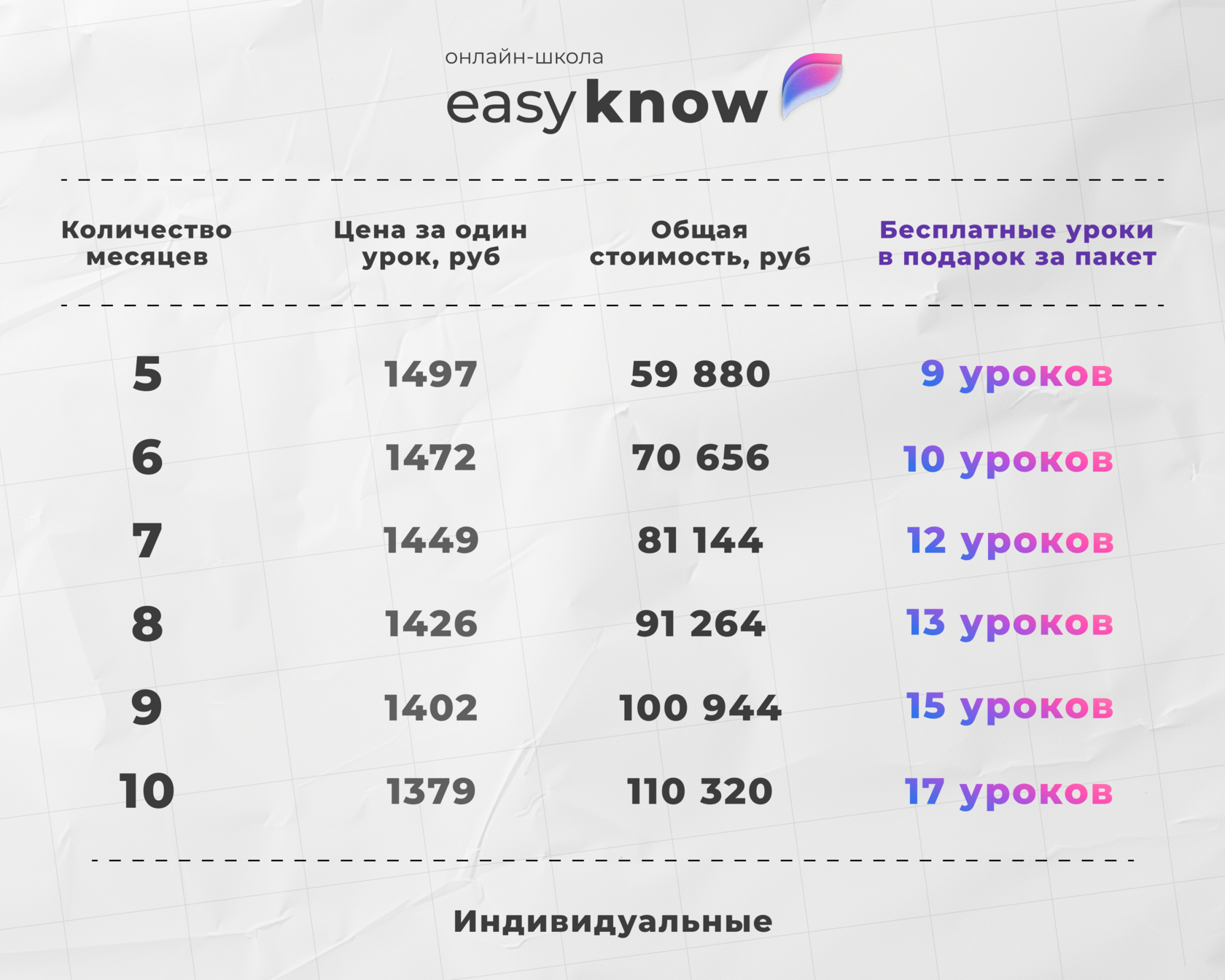
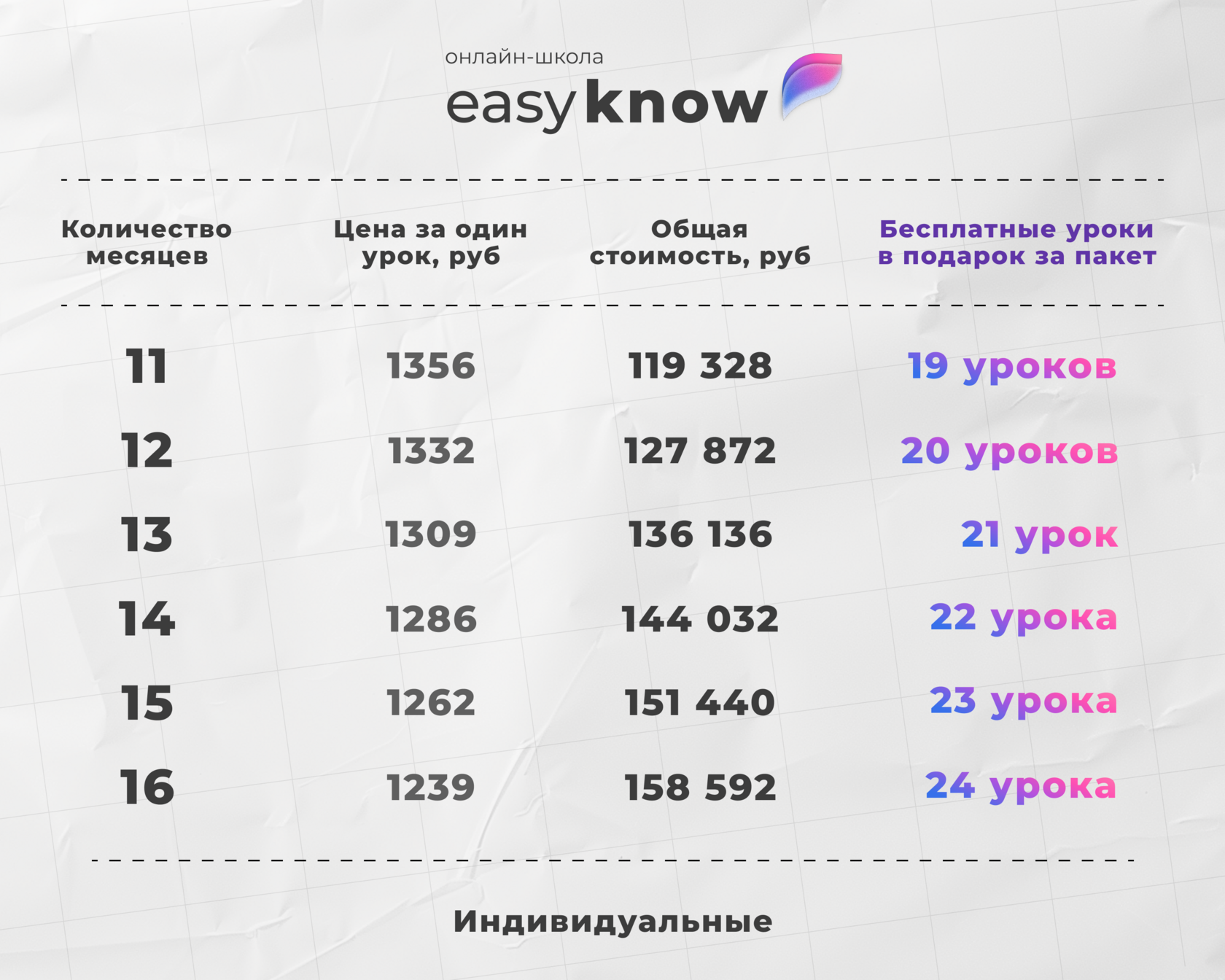
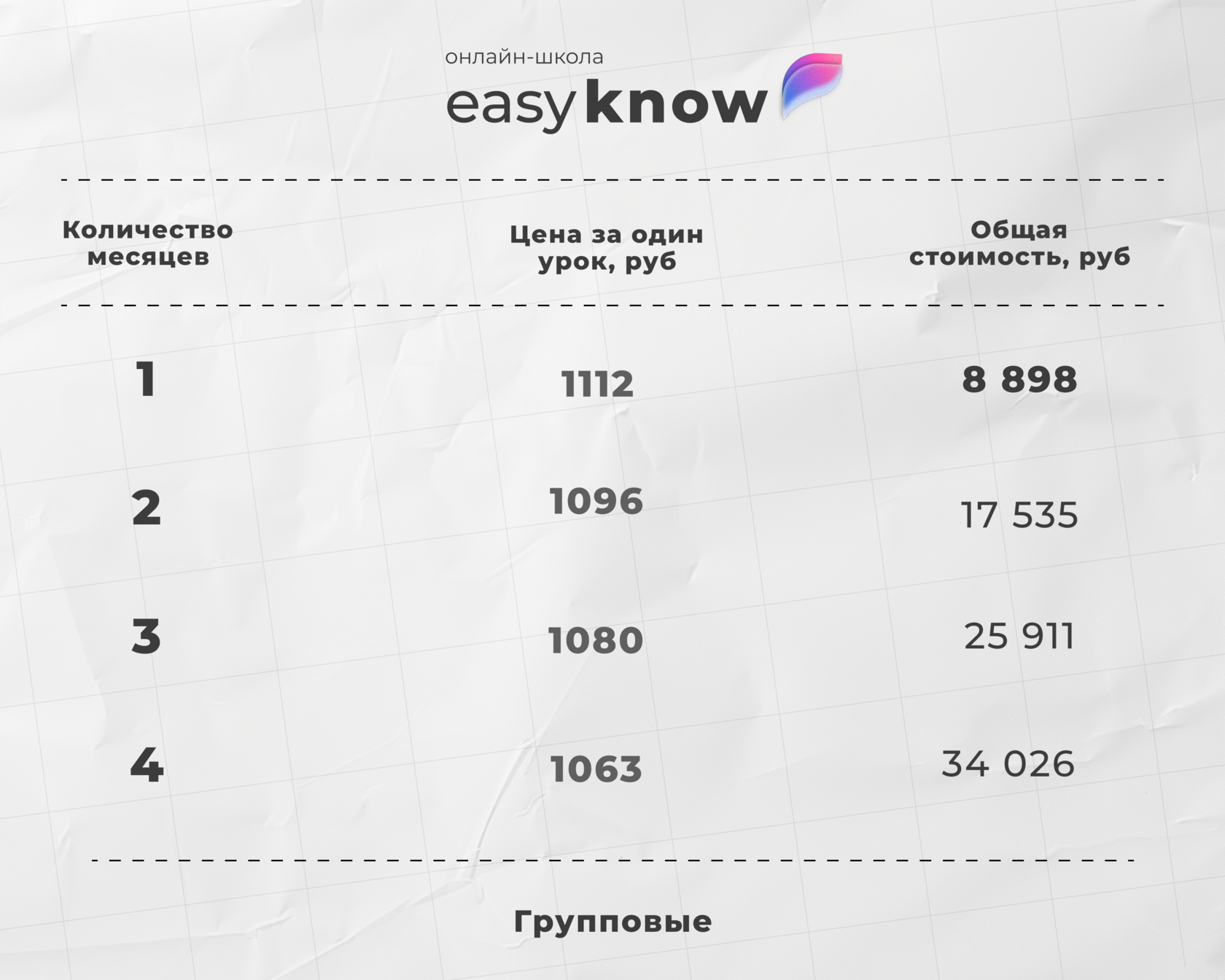
Подготовка на образовательной платформе

В онлайн школе Easyknow:

даём всю теорию по логарифмам для ЕГЭ;
учим применять свойства на практике;
занятия проходят онлайн с опытным репетитором;
образовательная платформа помогает системно готовиться и получать высокие баллы на экзамене.

Итог

Свойства логарифмов для ЕГЭ по математике — база для успешного решения заданий. Зная основные правила и тренируясь на примерах, можно быстро упростить даже сложные выражения. Подготовка с репетитором на образовательной платформе Easyknow поможет понять тему и уверенно сдать экзамен на высокие баллы.

Обучение в Easyknow

🎓 Репетиторство easyknow

Хочешь разобраться в теме быстро и без скучных объяснений?
Занимайся с преподавателем easyknow — индивидуально, просто и по твоему темпу.
Записаться на пробный урок

💬 Кураторство easyknow

Нужна поддержка в учебе, но не хочешь сразу на урок?
Подключи куратора easyknow — он поможет с задачами и объяснит непонятное прямо в мессенджере.
Получить помощь куратора